책의 예제 풀이가 부족한 것 같아 다시 풀어보고 이해한 내용을 정리하였다. 위 내용은 광학 1장과 2장 까지 학습 후 풀 수 있다. 문제 출처는 Jiun-Haw Lee, et al. <평판 디스플레이 공학>, 제2판 예제 2.1이다.
예제 2.1
완전 확산 표면은 관측되는 모든 각도에서 휘도가 일정하게 유지되는 표면으로 램버시안 표면이라고도 부른다. 예를 들어 표면이 거친 종이는 램버시안 표면에 매우 가깝다. 면적 A인 램버시안 표면에 조도가 E인 광원이 조명될 때, 표면의 휘도(L)을 구하라. 표면에서 모든 광이 완전히 반사된다. 즉, 입사광의 광속과 표면에서 반사되는 광속은 동일하다고 가정하라.
풀이
step1)
휘도(L, 단위 $cd/m^{2}$)은 단위면적 당(A) 광도(I, $lm/sr$)로도 간주할 수 있다. ($cd=\frac{lm}{sr}$)
$L=\frac{dI}{dA}$ (1)

문제에서 언급하기를, 램버시안 표면은 '모든 각도'에서 휘도가 일정하게 유지된다고 하였다. 그러나 관찰하는 각도에 따라 보이는 면적은 달라진다. ( $\theta$는 시야 방향과 표면 법선이 이루는 각이다)
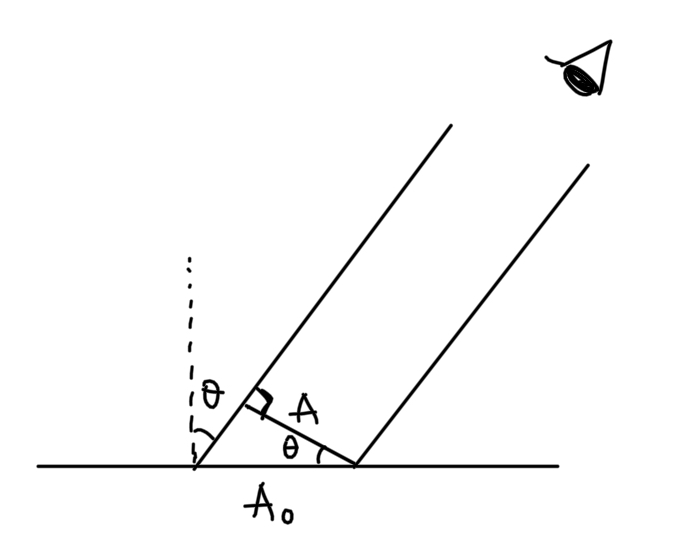
이는 정사영의 원리를 이용하여 $A_{0}$로부터 면적 $A$를 구할 수 있다.

따라서, 관측되는 각도에 따라 면적은 수직한 방향과 비교해서 $\cos\theta$ 만큼 작게 보인다.
$dA = dA_{0}\cos\theta$ (2)
여기서 $A_{0}$는 표면 법선 방향에서 볼 때 면적이다.
step2)
다시 (1)번 식으로 돌아가서, 램버시안 표면의 휘도는 모든 방향에서 동일하기 때문에, 광도는 다음과 같다. 여기서 $I_{0}$은 표면 법선 방향에서의 광도이다.
$I=I_{0}\cos\theta$ (3)
왜냐하면 (3)번 식을 (1)번 식에 대입해 다음 식이 성립하기 때문이다.
$L=\frac{dI_{0}\cos\theta}{dA_{0}\cos\theta}$ (4)
step3)
그렇다면, 우리가 아직까지 쓰지 않은 식이 하나 남았다. 문제에서 '입사광의 광속과 표면에서 방사되는 광속은 동일하다'는 조건을 사용해 보자.
$F_{in}=EA$ (5)
여기서 E(조도)는 Illuminance($lm/m^{2}$, 단위:lux)이다.
그럼 방사되는 광속(F_{out}, 단위: $lm$)은 어떻게 구할까? 광도(I)는 입체각 당 루멘($lm/sr$)으로 구한다. 광도를 입체각으로 적분하면 광속을 구할 수 있다.
$$\begin{align*}
F_{out} &= \int\mathrm{I}d\omega \\
&=\int I(\theta)d\omega \\
\end{align*} $$
여기서 $\omega$를 $\theta$와 $\phi$로 풀어주면 된다. 이는 광속이 둥근 구의 형태로 방사하기 때문에 구면좌표계의 이중적분을 활용한 것이다. 이에 관해서는 다음 포스팅을 참고하자.
구면좌표계 2중적분: 구의 면적 구하기
목차 1. 구면좌표계의 정의 2. 구면좌표계에서 2중적분1. 구면좌표계의 정의구(Sphere)란 공간좌표계의 한 정점으로부터 같은 거리에 있는 점들의 집합이다. 구의 반지름을 R이라고 할 때, 겉넓이 S
thelandofthe.tistory.com
아무튼, $d\omega = \sin \phi d\theta d\phi$ 이므로, (반지름 $\rho$의 길이를 왜 1로 퉁치는지는 아직까지 잘 모르겠다)
$$ \begin{align*}
&=\int \int I(\theta)d\phi d\sin \theta d \theta \\
&=I(\theta)\int_{0}^{2\pi}\int_{0}^{\frac{2}{\pi}}\cos \theta \sin \theta d\theta d\phi \\
&=2\pi\mathrm{I}_{0}\int_{0}^{\frac{\pi}{2}}\cos \theta \sin \theta d\theta \\
&= \pi\mathrm{I}_{0}\\
&=\pi\mathrm{L}\mathrm{A}
\end{align*} $$
왜 안쪽 적분의 범위가 0부터 $\pi$가 아니라 $ \frac{\pi}{2}$이냐면, 구의 겉넓이가 아니라 반구의 겉넓이를 구하기 때문이다. (표면 위에서 방사하는 빛을 생각해 보라)
앞서 말한 대로, 입사광의 광속과 표면에서 방사되는 광속은 동일하므로, 다음과 같은 식이 성립한다.
$$\begin{align*}
F_{in}&=F_{out}\\
EA &= \pi\mathrm{L}\mathrm{A}\\
\end{align*} $$
$\therefore E = \pi\mathrm{L}$
이렇게 조도(E)와 램버시안 표면이라는 특성을 고려하여 휘도를 구해 보았다.
물리적으로 생각해보았을 때, 각도에 따라 관찰하는 면적이 작아지면 그 면적으로 통과하는 광속 또한 작아지므로, 광도(I)도 작아진다. 그러나, 빛의 밝기인 휘도(L, $cd/m^{2}$)은 어느 각도로 관찰해도 동일하다. 램버시안 표면에서 조도(E)와 휘도(L)의 관계는 $\pi$의 배수이다. 따라서 조도(E, $lm/m^{2}$)또한, 어느 각도에서 관찰해도 동일하다.
'슬기로운 공대생활 > 광학' 카테고리의 다른 글
| Ch2. Wave Motion (파동운동) - 1차원 파동 (0) | 2024.05.07 |
|---|---|
| 4장. 색 측정 (0) | 2023.09.28 |
| 3장. 눈 (0) | 2023.09.27 |
| 2장. 측광 원리와 단위 (0) | 2023.09.21 |
| 1장. 광학 서론 (0) | 2023.09.21 |



