Introduction
빛은 파동인가 입자인가?
빛의 입자설
- localization.
- Exist in a well-defined region of space.
- photon : Quantum Mechanical view of light
👉 wave function (QM, 확률)
빛의 파동설
- Non-localization
- Classical traveling wave - self-sustaining disturbance of a medium, move through space trasporting energy and momentum (파동이 전달되는 매질이 스스로 지속되는 분포)
👉 Electromagnetic wave: classical eletromagnetism (Maxwell 방정식)
2.1 1차원 파동
역학적 파동(Mechanical wave)는 줄 위를 이동하는 파동, 수면 위를 이동하는 표면파, 공기로 전달되는 음파 등이 있다. 이는 두가지 wave로 분류할 수 있다.


• Longitudinal wave(종파) : 에너지가 전달되는 파동의 이동방향과 같은 방향으로 매질의 운동(변위)가 나타나는 파동 (ex sound wave)
• Transverse wave(횡파) : 에너지가 전달되는 파동의 수직방향으로 매질의 운동(변위)가 나타나는 파동 (ex. 전자기파)
위치와 시간의 함수로 표현

위 그림처럼 시간 t에 따라 +x 방향으로 진행하는 파동은 아래와 같이 표현할 수 있다


예를 들어, t=0에서의 분포는 다음과 같다.


펄스는 x축을 따라 vt만큼 이동한다.


위 식을 대입하면, Ψ 를 다음과 같이 정지된 S계와 관계된 변수들로 표현할 수 있다.

연습해보기
1.

위 식은 속력 v로 +x 방향으로 진행하는 파동을 의미한다.

2.
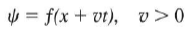
이건 파동이 -x 방향, 즉 왼쪽으로 진행하는 파동을 의미한다.
💡 위에서 설명했던 파동의 모양이 2차원이 아니라 1차원인 이유!
파동이 선을 따라서 이동하여 파동을 결정하는 공간변수가 한 개이기 때문이다
연못에 퍼지는 잔물결의 경우, 면을 가로질러 퍼져나가므로 두 개의 공간변수로 기술한다.
1차원 미분 파동방정식
1차원 파동방정식을 미분하면 다음과 같은 방정식을 얻을 수 있는데,
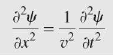
이 식이 의미하는 것은, 파동함수 Ψ1 과 Ψ2 가 각각 해이면, Ψ1+Ψ2도 해가 된다는 것이다. (중첩)
다시 말해, 어떤 함수가 파동방정식의 해이면, 그 함수는 파동을 나타낸다.
연습해보기
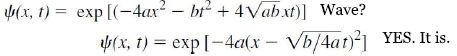
'슬기로운 공대생활 > 광학' 카테고리의 다른 글
| Ch2. Wave Motion (파동운동) - 위상과 위상속도 (0) | 2024.05.07 |
|---|---|
| Ch2. Wave Motion (파동운동) - 조화파 (0) | 2024.05.07 |
| 4장. 색 측정 (0) | 2023.09.28 |
| 3장. 눈 (0) | 2023.09.27 |
| [문제] 램버시안 표면의 휘도 구하기 (0) | 2023.09.27 |



