반도체 소자 기본 개념 이해하기

에너지 밴드 이론

출처: 이미지 클릭

 

🚩 전도대 (Conduction band)

절대온도 0K에서 전자가 존재할 수 없는 에너지 레벨

온도가 올라가면 전자들이 채워져 전류가 흐를 수 있게 하는 영역

 

🚩 가전자대(Valence Band)

절대온도 0K에서 전자가 전부 채워져있는 에너지 레벨

온도가 올라가면 전자들이 빠져나가 빈 공간(정공-hole)을 만드는 영역

 

🚩 에너지 밴드 갭(Energy Band Gap)

전자가 존재할 수 없는 에너지 레벨(영역)

 

에너지 밴드 이론으로 설명하는 도체, 반도체, 부도체의 차이

출처: 이미지 클릭

 

• 도체는 전도대와 가전자대가 겹쳐져 있기 때문에 작은 에너지로도 전류를 생성할 수 있다.

• 반도체는 일정 수준의 에너지를 외부에서 가해주어야 전류가 흐르게 된다.

• 부도체는 밴드갭이 너무 크기 때문에 전류가 흐르지 않는다. 

 

발광소자의 원리

 

반도체에 에너지를 가해주면 전자가 전도대로 점프를 한다. 그러나 모든 물질은 안정적인 상태로 돌아오려는 성질이 있기 때문에 낮은 에너지 준위인 가전자대로 내려오고 싶어한다. 

출처: 이미지 클릭

 

전자가 전도대에서 가전자대로 내려오면서 빛 또는 열(에너지)를 방출한다. 

 

페르미 함수와 DOS (Density of State)

전자 및 정공이 발견된 확률과 이것들을 담을 수 있는 공간에 대한 정보로 에너지 밴드 내에서 전자와 정공들의 분포도를 알 수 있다.

 

DOS (Density of States)

 

각 에너지 띠에 허용되는 상태의 수

 

출처: 이미지 클릭

 

•  gc(E): 전도대에서의 DOS

•  gv(E): 가전자대에서의 DOS

 

오른쪽 그래프에서 Ec는 높은 에너지일수록 자리가 더 많은 것을 알 수 있고, Ev에 대해서는 낮은 에너지일수록 자리가 더 많은 특징을 알 수 있다. 

 

 

페르미 함수

 

전자의 관점에서 전자가 그 에너지 준위에 존재할 확률. 특정 에너지 레벨에서의 전자가 존재할 확률.

 

 

 

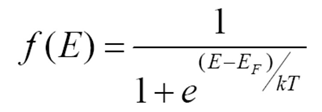
f(E) : 페르미 준위

T : 절대온도

k : 볼츠만 상수 (8.617*10^-5)

 

페르미 함수는 0~1 사이의 값을 가지게 되는데 전자가 존재할 확률이 100%에 가까우면 1과 가까운 값을, 0%에 가까우면 0에 가까운 값을 나타나게 된다.

 

💡 페르미 준위(Fermi level)란?

전자가 채워질 확률이 50% 인 지점

출처: 이미지 클릭

 

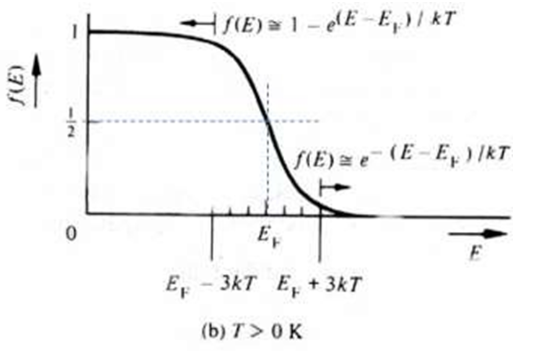
에너지가 커지면 전자가 채워질 확률, 즉 해당 에너지 준위에서 전자가 존재할 확률이 0에 수렴하고(전도대),

에너지가 작아지면 해당 에너지 준위에서 전자가 존재할 확률이 1에 수렴한다(가전자대).

 

💡 캐리어의 분포 구하기

DOS와 페르미 함수를 곱하게 되면, 전자 및 정공의 분포를 알 수 있다. 캐리어가 존재할 수 있는 상태의 수와 캐리어의 존재확률을 곱하게 되는 것이기 때문. 이를 통해 시스템이 N-type또는 P-type인지를 알 수 있다.

 

1. 페르미 레벨이 밴드갭의 거의 가운데에 있을 때

에너지밴드 다이어그램 / DOS / 페르미 함수 / 이 둘을 곱한 캐리어 분포

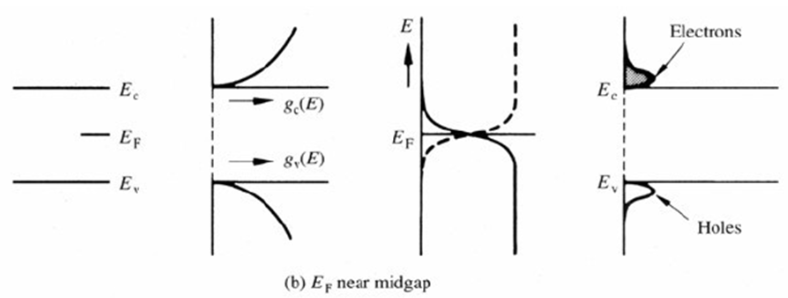
전자와 홀의 분포량이 거의 동일함.

ex) 도핑이 없는 intrinsic semiconductor에서는 f(E)는 거의 가운데에 위치해 있을 것

 

2. 페르미 준위가 전도대에 가까이 위치해 있을 때

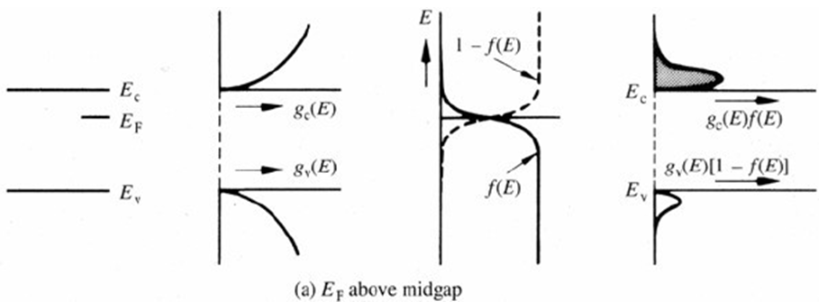
페르미 함수가 위로 치우져 올라가기 때문에 전자의 분포가 훨씬 많아진다.

ex) N-type 반도체 : 전자가 더 많음

 

3. 페르미 준위가 가전자대에 가까이 위치해 있을 때

 

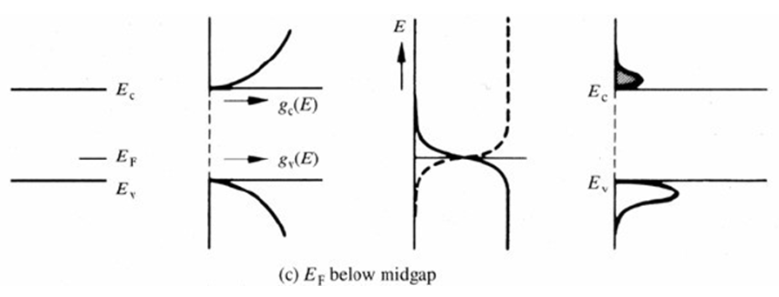
홀의 분포가 훨씬 크다는 것을 확인할 수 있음

ex) P-type 반도체 : 정공이 더 많음

 

 

출처:

(1) 반도체와 디스플레이의 기초이론 - 에너지 밴드.. : 네이버블로그 (naver.com)

(2) #02 쉽게 알아 보는 페르미 함수, 상태밀도 (tistory.com)